
图形推理
以下是图形推理的完整解题框架和技巧总结,结合历年真题高频考点整理而成:
一、四大核心解题思路
-
图形相似且元素相同——看位置变化
适用特征:图形整体框架一致,元素位置改变
-
图形相似但元素有增减——看叠加规律
典型特征:存在部分重合元素
- 去同存异(保留差异部分)
- 去异存同(保留相同部分)
- 规律叠加(黑白运算常见)
-
图形差异大且独立——先查属性后看数量
(1)几何属性分析:
-
对称性:轴对称(注意对称轴数量/方向)、中心对称
-
直曲性:全直线/全曲线/混合型
-
封闭性:开放图形/封闭区域数
(2)数量关系分析(按考察频率排序):
- 面:封闭区域数(图1有3个封闭区)
- 线:直线/曲线数、笔画数(奇点数÷2)
- 点:交点总数、特殊交点(十字点、切点)
- 角:直角数为主
-
多元素组合图形——先看分布后算数量
- 元素遍历:元素种类/位置重复出现
- 相对位置:相邻/相隔、相交/相离
- 元素传递:部分元素规律性变化
二、特殊题型处理技巧
-
立体图形
- 折纸盒:相对面排除法(同行隔一个、Z字两端)
- 三视图:注意遮挡关系和投影轮廓
-
汉字/字母题
- 结构特征:左右/上下结构、封闭区域数
- 笔画数:按标准书写笔画计算
-
阴影类题目
- 面积占比:阴影部分与整体比例关系
- 位置移动:阴影沿特定路径平移
三、实战解题步骤
- 快速扫描建立初步判断(相似/相异)
- 按特征锁定解题方向(参考上述四类思路)
- 验证规律时注意:
- 优先验证高频考点(如面的数量>对称性)
- 规律需在整组图形中普遍适用
- 注意选项差异点验证规律有效性
高频易错提示:
① 旋转与翻转易混淆→用"画箭头法"区分
② 笔画数计算易漏奇点→端点都是奇点
③ 复合考点常出现→如对称+数量组合考
真题示例解析:
【2021国考真题】九宫格图形中,第三行前两图封闭区数分别为3、4,遵循行内相加规律,?处应为3+4=7个封闭区,对应选项B
建议训练方法:
- 每天10题保持题感
- 建立错题本记录特征规律
- 考前重点复盘高频考点图例
图形推理的常见考点有哪些?
图形推理的常见考点可分为六大类,结合高频考题和解题技巧,具体如下:
一、位置类考点
-
动态位置变化
- 平移:元素沿固定方向(上下、左右、循环)移动,注意移动路径的折返规律
- 旋转:顺时针/逆时针旋转(常考45°、90°、180°),用"时针法"判断方向
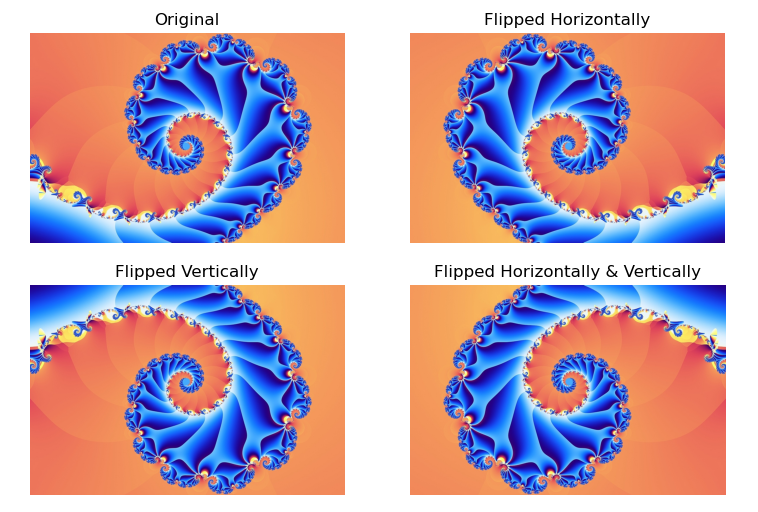
- 翻转:水平/垂直轴对称翻转,需区分与旋转的差异
-
静态位置关系
- 相离:相邻、相隔、上下布局
- 相交:形状、面积、交点数
- 包含:内外位置(如直线图形包含曲线图形)
二、样式类考点
-
叠加运算
- 去同存异(保留差异部分)
- 去异存同(保留相同部分)
- 黑白叠加(如黑+白=灰)
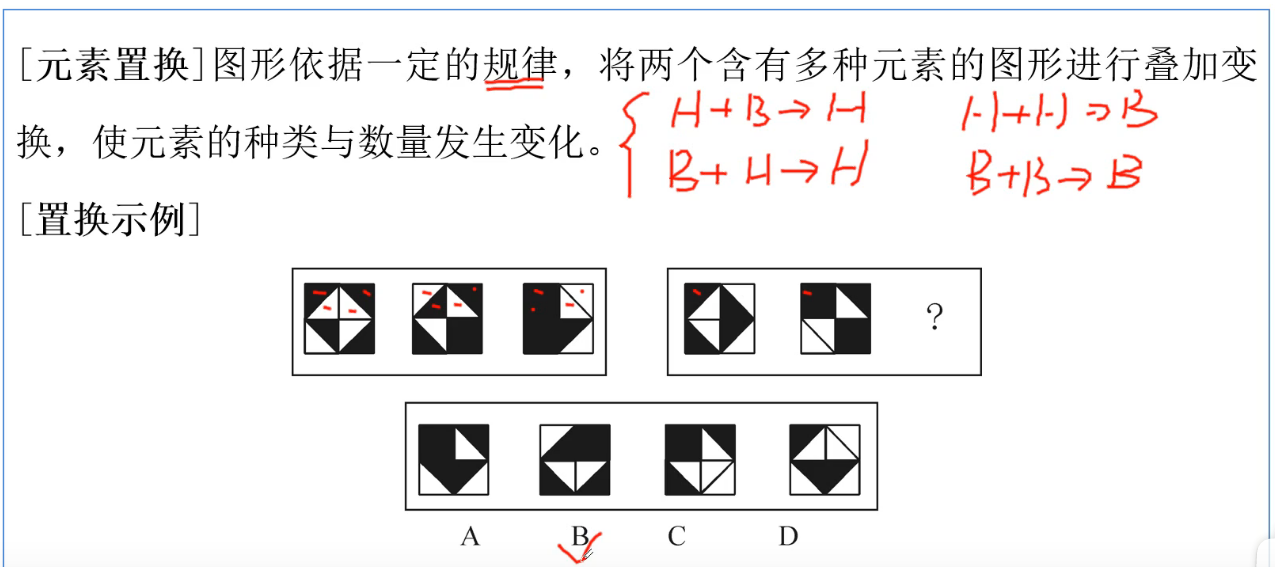
-
元素遍历
- 单元素遍历:不同图中重复出现某元素
- 整体遍历:以行/列为单位补全元素
三、属性类考点
-
对称性
- 轴对称(对称轴数量/方向变化)
- 中心对称(如平行四边形)
- 复合对称(如正六边形既轴对称又中心对称)
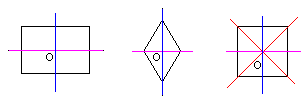
-
曲直性与封闭性
- 全直线/全曲线/混合型
- 开放图形、封闭区域数(高频考面数量)
四、数量类考点(高频核心)
-
面:封闭区域数(如汉字中的“口”算1个面)
-
线:
- 直线/曲线数
- 笔画数(奇点数÷2,端点均为奇点)
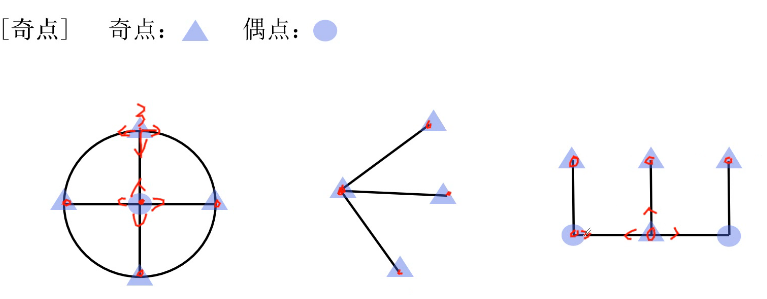
-
点:
-
角:直角、锐角、钝角数量变化
五、特殊规律
-
图形间关系
-
功能元素
六、空间重构
-
六面体展开图
- 相对面排除法(Z字两端、间隔一个)
- 时针法判断相邻面
-
三视图与截面图
- 主视/俯视/左视图的遮挡关系
- 常见立体图形截面形状(如圆柱截面为椭圆)
高频解题技巧
-
优先级策略:
- 先查属性(对称、曲直),再验数量(面>线>点)
- 动态位置>叠加>遍历
-
图形敏感训练:
- 对称图形、五角星、日/田字变形图、多交点图形需重点注意
-
选项差异验证:
- 若两个选项符合同一规律,需对比细节差异点(如某个交点数)
示例:若题干图形均含3个封闭区,则优先验证选项的面数量是否为3。
通过系统掌握这些考点,结合每日10-20题的针对性训练,可显著提升图形推理的解题速度和准确率。考前需重点复盘错题中的规律误判点,强化高频考点敏感度。
图形推理中,动态位置变化的具体应用有哪些?
在图形推理中,动态位置变化是高频考点之一,其核心特征是图形元素组成相同,仅位置发生规律性变化。以下是具体应用场景及解题技巧的详细总结:
一、平移规律
适用特征:元素沿固定路径移动,常见于九宫格、田字格或循环排列的图形中。
- 方向与路径:
- 基本方向:上下、左右、对角线
- 复杂路径:折返(如“Z”字型)、循环(移动到边界后返回起点)
- 示例:黑点沿外框顺时针每次移动一格
- 步数规律:
- 常数列:每次移动固定步数(如每次移动1格)
- 等差数列:步数递增或递减(如1→2→3)
- 真题示例:三角形在六边形内部逆时针移动1格,五角星顺时针移动2格
二、旋转规律
适用特征:元素绕固定点转动,形状不变但方向改变。
- 判断方法:
- 时针法:画时针方向一致则为旋转(不一致则为翻转)
- 箭头法:标记元素方向,观察角度变化
- 常见角度:
- 30°、45°、90°、180°(以90°最频繁)
- 示例:外层元素沿五边形边顺时针旋转1格,中层元素逆时针旋转90°
- 复合旋转:
- 多元素同步旋转(如整体+局部旋转)
- 真题示例:图形整体逆时针旋转90°,再对局部元素翻转
三、翻转规律
适用特征:图形关于某条轴对称,形状镜像反转。
- 对称轴类型:
- 水平翻转(上下对称)
- 垂直翻转(左右对称)
- 示例:前三个图形通过旋转变化,第四个图形为垂直翻转
- 区分技巧:
- 对比相邻图形差异,若无法通过旋转得到则为翻转
- 真题示例:阴影三角形整体沿直线逆时针翻转,形成镜像对称
四、综合应用与解题技巧
- 优先级策略:
- 元素相同且位置变化明显时,优先考虑动态位置
- 九宫格题目优先观察行/列内移动规律
- 复合规律识别:
- 平移+旋转(如元素移动同时自身旋转)
- 旋转+翻转(如先整体旋转再局部翻转)
- 易错点提示:
- 平移路径需注意循环或折返,避免误判为增减元素
- 区分旋转与翻转时,务必使用时针法验证
五、典型真题解析
【例1】(2020联考)找出不同规律的图形:
- 题干:四个图形中三个为旋转,D为垂直翻转
- 解法:通过时针法判断方向差异,锁定翻转图形
【例2】(2021上海)阴影三角形规律:
- 规律:三角形逆时针翻转+沿直线移动
- 关键:对比镜像对称关系,排除旋转选项
总结
动态位置变化的核心在于观察元素移动轨迹与方向,通过标记关键点、对比相邻图形差异快速锁定规律。日常训练需重点关注九宫格、田字格题型,强化对平移路径和复合旋转的敏感度。
动态位置变化中如何识别和处理不同图形元素的位置变化?
在图形推理中,动态位置变化的识别与处理需结合元素特征和规律类型,以下是具体方法及示例:
一、识别动态位置变化的三大要素
-
元素组成一致性
图形元素种类、数量、形状完全相同,仅位置或方向改变。
示例:九宫格中三角形、圆形等元素在固定框架内移动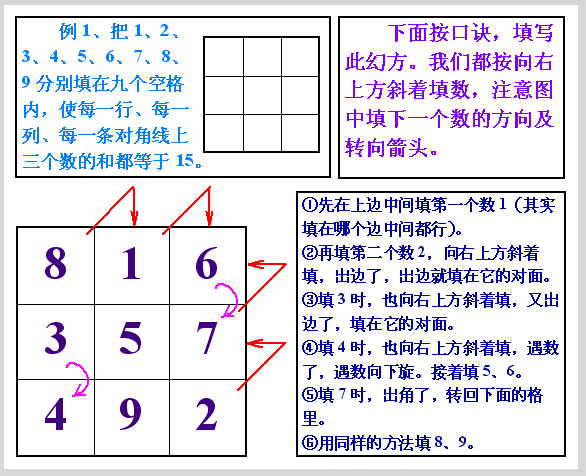
-
变化类型判断
- 平移:观察元素沿固定路径移动(如循环、折返),步数常为等差数列。
例:阴影沿外框顺时针移动1格,空白区域逆时针移动2格
- 旋转:利用时针法标记元素方向,验证角度(如45°、90°)。
例:外层元素顺时针旋转,内层箭头逆时针旋转90°
- 翻转:对比对称轴关系(横轴/竖轴),注意镜像特征。
例:三角形整体垂直翻转后与原图形成轴对称
-
复合变化处理
当多个元素同步变化时,需分元素单独分析:
1. **分解图形**:标记不同元素(如编号1、2、3);
2. **独立追踪**:观察各元素的移动路径;
3. **组合验证**:检查整体规律是否自洽。
示例:九宫格中黑点循环移动,白色方块按对角线平移
二、处理不同元素的动态位置变化
-
多元素分轨处理
- 优先级策略:先分析移动路径明显的元素(如黑块、箭头),再处理次要元素。
- 路径冲突解决:若元素移动轨迹重叠,优先验证步数是否遵循等差数列。
例:黑块逆时针移动1格,白块顺时针移动2格,互不干扰
-
复合规律识别
- 平移+旋转:元素移动同时自身旋转(如箭头移动时方向改变)。
例:三角形沿六边形平移,同时每步自转90°
- 旋转+翻转:先整体旋转再局部翻转(如九宫格第三行规律)。
-
特殊图形处理技巧
- 阴影/空白区域:关注面积占比变化,结合位置移动分析;
- 嵌套结构:外层元素控制框架移动,内层元素独立变化(如钟摆模型)。
三、高频易错点与验证方法
-
易混淆规律区分
- 旋转vs翻转:用时针法标记方向,一致为旋转,不一致为翻转;
- 循环vs折返:观察元素到达边界后是否原路返回或跳转起点。
-
验证工具
- 箭头标记法:在草图上标注元素移动方向;
- 编号追踪法:对相同元素编号后对比位置变化。
四、真题示例解析
【例】(2021联考)
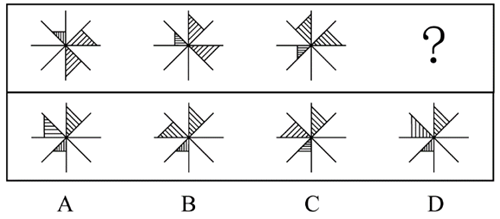
分析:
- 组成元素相同(三个三角形),方向变化明显;
- 用时针法标记三角形顶点,发现整体逆时针翻转;
- 验证相邻图形差异,排除旋转选项。
答案:B
总结
处理动态位置变化需:
- 分解元素,独立分析移动规律;
- 复合变化优先验证高频组合(平移+旋转);
- 标记验证避免混淆(如箭头法、编号法)。
系统训练可参考材料中的九宫格与多元素分轨题型。
在样式类中,遍历是如何应用的,它通常涉及到哪些元素?
在图形推理的样式类遍历规律中,其应用核心是通过元素种类与数量的完整性补缺来解题,具体应用方式和元素特征如下:
一、遍历规律的应用条件
-
元素组成相似性
所有图形需具有相同种类和数量的元素(如圆形、三角形、箭头等),仅排列组合顺序不同。
示例:题干三幅图均含○、□、△各一个,但位置排列不同
-
补缺逻辑驱动
通过观察已知图形中元素的出现频次,推断缺失图形应包含未重复出现的元素组合。
示例:若前两图已出现○、△,则第三图需补□
二、典型应用场景与元素类型
1. 基础几何元素遍历
- 常见元素:圆形、三角形、正方形、菱形、五角星
- 应用示例:
九宫格每行需包含全部基础元素,第三行缺少△时需补入
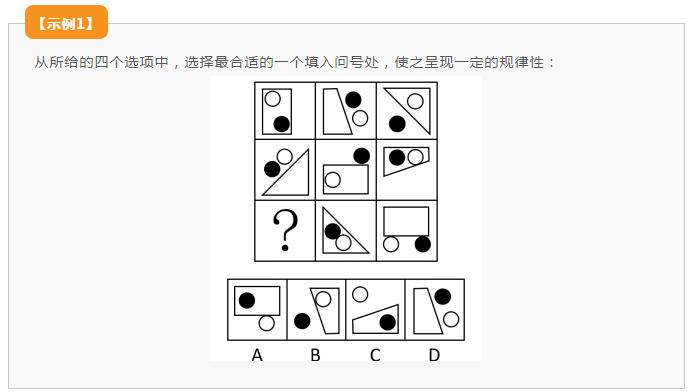
2. 线条方向遍历
- 元素类型:横线、竖线、斜线(/、\)
- 真题模式:
每行需包含所有方向线条,若第三行已有横、竖线,则问号处补斜线组合
例:选择含“/”和“\”的图形(参考材料3†第三段解析)
3. 复合符号遍历
- 元素类型:箭头、特殊符号(如◆、●)、汉字部件
- 嵌套规律:
元素可能以嵌套形式出现(如大圆套小三角),需同时验证外层与内层元素完整性
三、解题步骤与验证技巧
-
第一步:识别遍历特征
- 对比图形元素种类与数量,确认无新增/缺失元素(如三幅图均含3种元素)
- 排除位置类平移、旋转等干扰规律
-
第二步:定位缺失组合
- 横向对比:在九宫格中按行/列统计元素出现情况
- 纵向补缺:若某行已有○、□,则补△;若某列已有横、竖线,补斜线
-
第三步:样式差异验证
- 检查补入元素是否符合题干样式变化趋势(如线条粗细、阴影方向)
- 排除与已知元素重复排列组合的干扰选项
四、高频易错点
-
元素数量误判
- 错误:将多个相同元素(如两个○)视为一个种类
- 纠正:明确遍历要求种类一致而非数量一致
-
复合规律干扰
- 错误:将遍历与旋转混合(如三角形旋转后误认为新元素)
- 纠正:用标记法固定元素编号,排除方向干扰
-
嵌套结构遗漏
- 错误:忽略内外层元素需分别遍历
- 纠正:分层分析(如外层遍历○□△,内层遍历箭头方向)
真题解析示例(参考材料3†)
题干:
第一行图形含○、□、△,第二行含相同元素但排列不同,第三行已显示○、□
解法:
- 识别每行需包含○、□、△三类元素;
- 第三行缺△,排除不含△的选项;
- 验证△的样式(如是否带阴影)与题干一致。
答案:选择含△且样式匹配的图形
通过系统性训练可快速识别遍历规律,重点关注元素完整性和排列差异性两大特征,结合分层验证提升准确率。









